Основы статистической теории радиолокации

Если о сигнале все известно , то нет необходимости в его приеме, если о нем ничего не известно, то его невозможно отличить от помех, и прием его невозможен.

Поэтому, как правило, информацию содержат создаваемые объектом наблюдения и средой, неизвестные в месте приема, изменения параметров сигнала, т.е. в месте приема существует некоторая априорная информация

об исходных значениях информационных параметров.

Прием сигнала должен увеличивать сведения о нем. Сведения после приема называют апостериорными

и используются для принятия решения.

Неизбежные помехи и искажения в радиолиниях приводят к ошибкам в принимаемых решениях. Задача состоит в построении такой радиосистемы, которая бы уменьшала эти ошибки до минимума.

Эта задача может решаться на двух уровнях:

- для каждого заданного вида сигнала ищут приемник, сводящий ошибки к теоретическому минимуму. Такой приемник называется оптимальным

для данного вида сигнала, а даваемый им минимальный уровень искажения, содержащейся в сигнале информации, определяет потенциальную помехоустойчивость

, причем помехоустойчивость любого реального приемника не может ее превысить.

- полагая, что каждый сигнал обрабатывается оптимальным для него приемником, ищут пару сигнал - оптимальный приемник, для которой ошибки минимальны.

Таким образом, если на первом уровне оптимизируется только приемник, то на втором - вся радиосистема.

Для систем извлечения информации характерен системный подход к задаче оптимизации, соответствующей второму из указанных уровней.

Типовая схема прохождения сигнала в одноканальной радиолинии измерения приведена на рисунке 1.

Рисунок 1

- измеряемый параметр (дальность, скорость, угловые координаты и т.д.);

- электрический параметр (частота, фаза, амплитуда и т.д.);

- радиосигнал, зависящий не только от времени и информативного параметра , но и от неинформативных параметров;

- неинформативные параметры;

- внешняя помеха, воздействующая на радиолинию;

- внутренние шумы в приемном устройстве;

Различают три характерных частных случая сигналов:

- сигнал известен точно;

- сигнал со случайной начальной фазой;

- сигнал со случайной начальной фазой и амплитудой;

- результирующее воздействие на входе приемника, в общем случае сложная функция сигнала и обеих помех, в простейшем случае - аддитивная сумма;

- решающий алгоритм обработки этого искаженного помехами сигнала, позволяющий принять то самое решение.

Традиционно используют два этапа обработки :

- этап первичной обработки, обеспечивающий выделение из входного воздействия полезного сигнала, его демодуляцию и измерение параметров;

- этап вторичной обработки, обеспечивающий определение траекторий движения объекта;

В последнее время в связи с развитием сложных комплексов систем извлечения информации, разнесенных в пространстве и (или) времени, из этапа вторичной обработки выделяют как самостоятельный этап, обеспечивающий совместную обработку данных об избранных целях, полученных от разных систем в различное время. Решение должно быть выработано и передано в наиболее удобном для использования виде в индикаторное или регистрирующее устройство, либо ЭВМ или линию связи.

По виду принимаемого решения различают 5 основных задач:

. Различение

сигналов и обнаружение

. Возможны сигналов с априорными вероятностями , причем всегда на вход приемника поступает один из сигналов, т.е.:

Необходимо по результирующему входному воздействию за время наблюдения определить с минимальной ошибкой, какой из сигналов принят. При задача различения сигналов вырождается в более простую - задачу обнаружения, сводящуюся к принятию решения о том, есть сигнал или его нет.

2. Оценка параметров сигнала

. Электрический параметр сигнала имеет априорное распределение вероятностей и изменяется столь медленно, что , т.е. за время наблюдения .

Необходимо по за время определить с минимальной ошибкой переданное значение .

Принято различать точечное оценивание, осуществляемое по результатам единичного замера, и следящее, при котором оценка уточняется путем учета результатов предыдущих замеров.

3. Фильтрация параметра сигнала

. Электрический параметр сигнала представляет собой случайный процесс с известными статистическими характеристиками, претерпевающий за период наблюдения существенные изменения. Необходимо по за время определить с минимальной ошибкой, какая из реализаций или самого сигнала передана.

Следящее оценивание параметра может трактоваться как один из вариантов его фильтрации. В частном случае, когда фильтрация вырождается в точечную оценку параметра .

4. Разрешение сигналов

. Возможен прием сигналов с вероятностями , причем несколько сигналов могут поступать на вход приемника одновременно, т.е. . При этом в предельном случае:

Необходимо по за время с минимальной ошибкой разделить все поступившие на вход приемника сигналы , а в ряде случаев и оценить их параметры.

5. Отождествление данных.

Несколько разнесенных в пространстве и (или) во времени радиосистем принимают искаженные помехами сигналы одной и той же цели: . Необходимо за время с минимальной ошибкой объединить полученные от разных систем данные об яркой цели. Кроме того, можно оптимизировать совместное решение двух и более видов задач и, в частности, задач обнаружения и оценки или фильтрации параметров сигнала.

Некоторые соотношения теории вероятностей

Моментные функции

а) Среднее значение:

- постоянная составляющая случайного процесса.

б) Средний квадрат:

Удобнее пользоваться центральной моментной функцией второго порядка, которая дает величину дисперсии случайной функции относительно среднего значения:

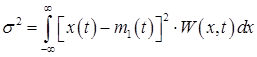- средняя мощность флуктуаций.

Характеристики и не дают достаточно полного представления о характере случайного процесса. Для дополнительной характеристики вводят понятие смешанной моментной функции второго порядка - корреляционной функции.

- двумерная функция распределения случайного процесса .

Наряду с усреднением по совокупности реализаций широко пользуются усреднением по времени.

Стационарный процесс - процесс, для которого функция распределения инвариантна к началу отсчета времени, т.е.:

Т.е. статистические свойства неизменны во времени. Такие процессы называются стационарными в “узком смысле”. Процессы, у которых инвариантны к началу отсчета математическое ожидание и корреляционные функции, называются стационарными в широком смысле.

Эргодический процесс - это стационарный процесс, для которого усреднение по совокупности реализаций дает тот же результат, что и усреднение по времени.

Для эргодических процессов (а стационарные процессы в большинстве являются эргодическими):

- постоянная составляющая;

- мощность случайного процесса;

- автокорреляционная функция;

- коэффициент корреляции.

Связь между корреляционной и спектральной характеристиками:

- энергетический спектр (прямое преобразование Фурье);

- обратное преобразование Фурье;

- дисперсия.

. Независимые случайные величины, для них справедливо:

- совместная плотность вероятностей.

и независимые случайные величины.

. Функционально связанные величины: .

Если известно распределение , то функция распределения - производную нужно брать по абсолютному значению, т.к. функция распределения всегда неотрицательна.

. Условные распределения - т.е. решается задача определения вероятности того, что случайная величина будет находиться в интервале и при этом случайная переменная будет заключена в интервале .

где: - двумерный закон распределения случайных переменных и , - соответствующие одномерные законы.

. Белый шум - это стационарный случайный процесс , функция корреляции которого равна - функции, умноженной на - спектральную плотность.

Этот процесс характеризуется тем, что значения в любые два, сколь угодно близкие моменты времени некоррелированы.

Спектральная плотность: . Спектральная плотность постоянна на всех частотах.

Примеры функций распределения:

- нормальный закон распределения (закон Гаусса);

- закон Релея.

Читайте также

Проектирование системы автоматического управления очистки стекла спортивного самолета
Задачи по управлению тем или иным явлением или процессом, возникающие в повседневной практической деятельности человека обширны и многообразны. Управление можно определить как совоку ...

Проект внутризоновой ВОЛП на участке Новосибирск—Карасук
Научно-технический прогресс во многом определяется скоростью передачи информации и ее объемом. Возможность резкого увеличения объемов передаваемой информации наиболее полно реализуется ...

Назначение и виды ударно-контактных извещателей
Извещатели ударно-контактные формируют тревожное извещение при нормированном ударном воздействии на контролируемую поверхность охраняемого объекта. Они предназначены для обнаружения раз ...

Основные разделы